FAME: a factorisation-aware matrix element emulator
Particle Physics, Machine Learning
The Large Hadron Collider (LHC) is an international high energy particle collider, operating at CERN, deep underground between the French-Swiss border. In order to test our theoretical model of nature, the Standard Model, we make use of simulated particle collision events in order to match those recorded in real life as closely as possible.
Simulating events is a procedure involving a long chain of many stages. One of the key steps is the evaluation of the actual scattering of particles embedded in what we call the matrix element. Traditional methods to compute this quantity, while sophisticated in technique, are computationally expensive and so are a time bottleneck. As an example, some of the collisions I worked on took around a minute to evaluate. This accumulates extremely rapidly when you require a billion simulated events to match the sample size of the experiment.
My thesis was focused on applying deep neural networks to build an emulator for these matrix elements in order to boost the rate at which we can generate simulated events. The key idea was to combine our from-first-principles knowledge of the structure of matrix elements, with the rapid advancements in machine learning. As a proof of concept, I published two papers [1][2] showing the viability of this method. For this work I was invited to speak at ACAT 2022 – the 21st International Workshop on Advanced Computing and Analysis Techniques in Physics Research.
For the particles physicists: these proof of concept papers were for electron-positron annihilation into up to 5 jets at tree-level and one-loop level. We exploit the factorisation property of matrix elements in soft and collinear limits, and utilise Catani-Seymour dipole functions/antenna functions, as a set of ‘basis’ functions to circumvent the neural network having to model these singular structures. In doing so, the neural network models a set of coefficients that are non-divergent and are well-behaved across the entirety of the sampled phase-space.
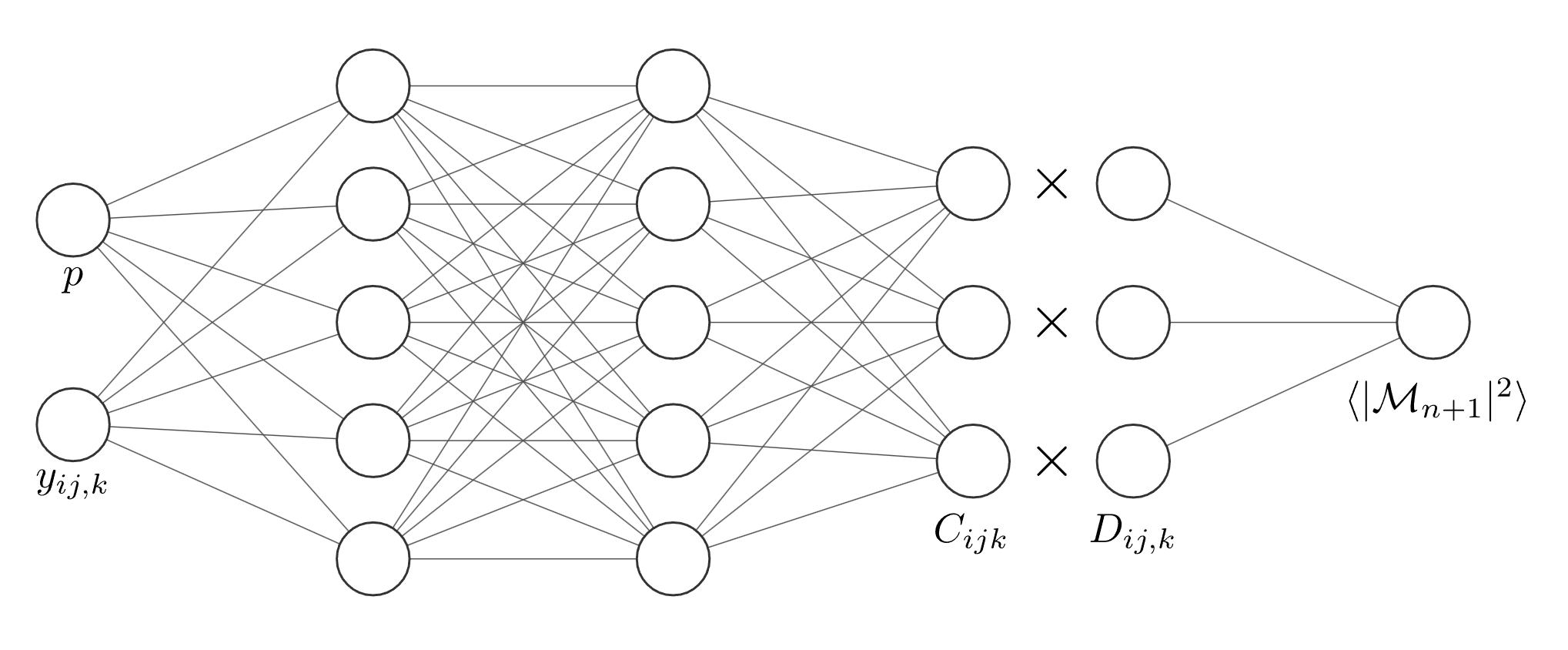The factorisation-aware model architecture
Since we exploit the factorisation property of matrix elements, we dub this the factorisation-aware model. We showed that with this new method, we were able to achieve 1% levels of accuracy in the emulation model whilst speeding up evaluation of matrix elements by up to 10000 times for the most complicated cases.
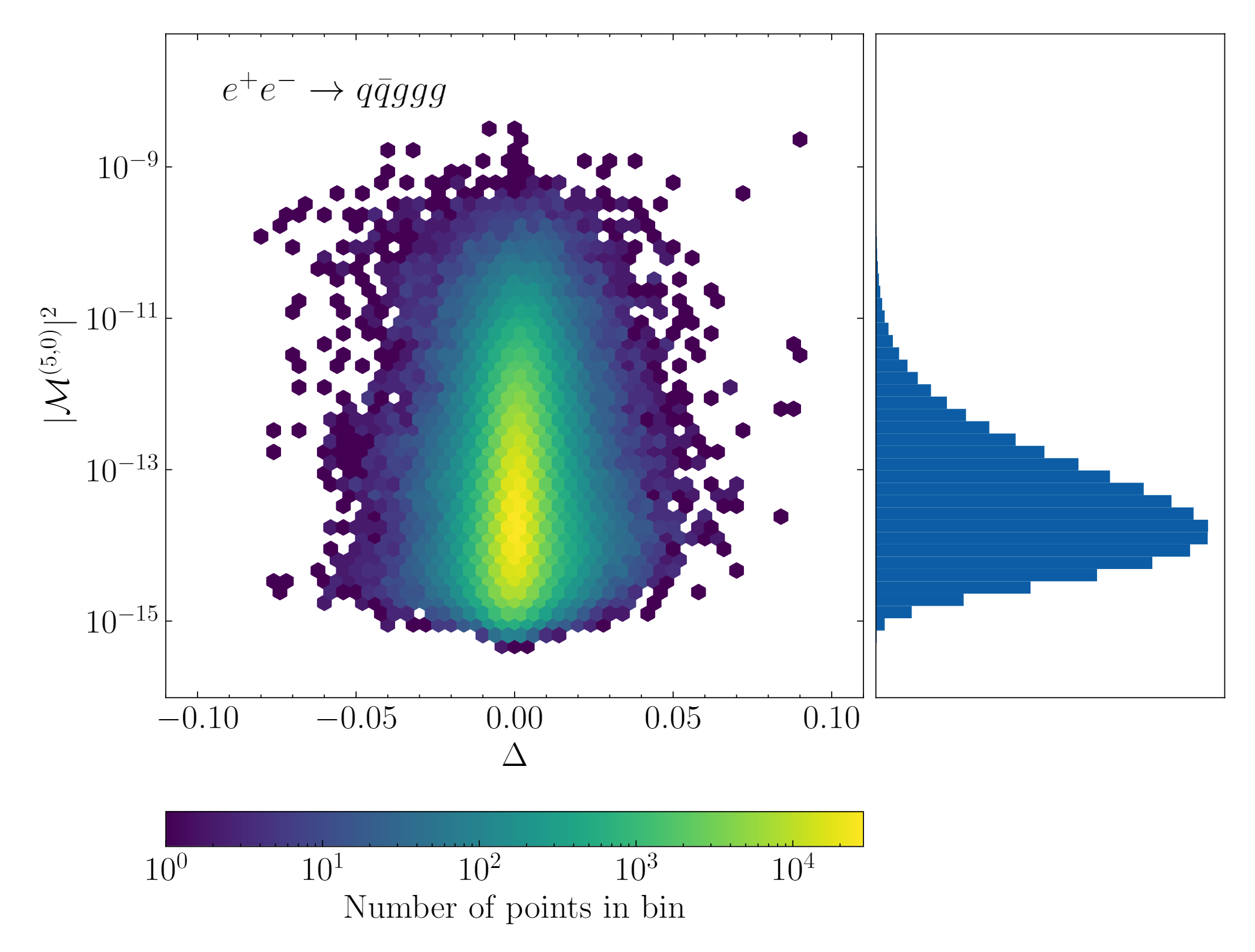Prediction accuracy: bulk of the points are in yellow bins with very low error
This work relied on extensive use of the Python machine learning ecosystem to bring the model to fruition. In particular, the model was built using the TensorFlow framework with the Keras front end, where I wrote custom code to construct the factorisation-aware architecture. Additionally, the software to generate the datasets required for model training and testing were written from the ground up, leveraging NumPy, multiprocessing, scikit-learn, to name just a few packages.
The code for these projects can be found on my GitHub:
The viability of embedding this neural network model into a real production environment was studied in the article [3] where I extended the model for the types of collisions actually being studied at the LHC. The key takeaway points from this study were that the flexibility of the model architecture allowed me to readily adapt the code for the new scenario, and that there was a speed-up of up to 350 times in generating simulated events for the most computationally expensive case we studied! To achieve these speed-ups, we made use of the C++ interface to the ONNX runtime which was much more performant, speedwise, compared to TensorFlow’s inference interface.
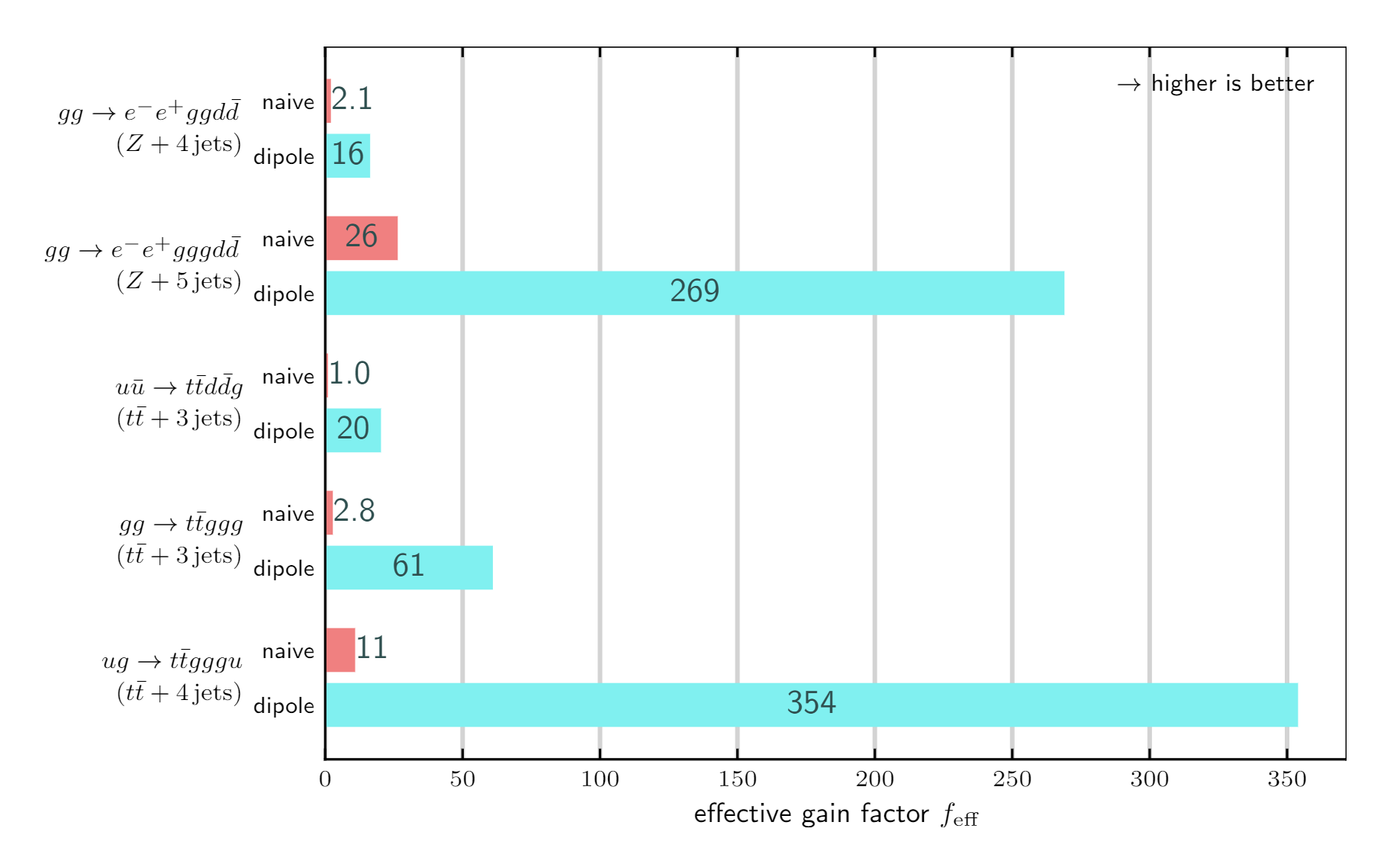Effective speed-up of factorisation-aware model labelled as ‘dipole’ compared to a simple neural network labelled as ‘naive’.